Purpose
Before starting a deep analysis, we must first explain and clarify the
purpose of the learning procedure.
What is learning and why do we need to achieve it?
We learn in order to avoid to do it again. Our conception of our
environment depend heavily on our capacity to perceive and therefore
comprehend our environment. In order to do both, we need to have a correct
balance: we need to minimize the error in such a way that the probability to
make adjustment is less than it was.
Are we really willing to learn if we know that we shan't be needing it
anymore?
On the counter part, we have also to answer the following: Should we
learn a process we know we have nearly no chance to use further? We can
then talk not of learning but also adjusting some values in order to satisfy
our immediate constraints.
We name contradiction I/O values a process for which the same
inputs is requested different outputs. For such process, we have several
reactions:
- The older outputs are to be abandoned in the profit of the new outputs. This
mean we have made a mistake and are correcting it.
- But what if output O(1) was requested at t(i) - then output O(0) at t(i+k), the output O(1) at t(i+ak) etc... we clearly notice we are going
to an endless loop and never the process will ever be correct. We have
then to ask ourselves if we are in fact dealing with all the concerned
input. Our learning is then not adjusting values but finding the
correct neuron we have to add in order to reach the requested result
and to be able to change the new input values to reach the previous
answer.
Learning Types
We can now understand that learning does not only concern modify the
ratio associated with the dendrite and that learning can result in different
actions for different purposes.
- Adjust the process is to adapt the ratios values of the
weight to reach the
requested value.
- Historical adjustment is to adjust the process and all the
recorded (input . output) associated pairs in such a way the result
would be the one expected. No concern is made of the error.
- Incremental adjustment is widening the process (except the
output) and attempting to find the neurons that when added to the
process will generate the requested output - on the other hand the past
output will also be satisfied - we have then to find the values of the
newly added neuron.
- Learning is concentrated on adapting the ratios of the
dendrite in such a way that the error of the I/O values is less than the
average error of the training set associated with the process.
- Historical learning is to apply the learning on the new
training set in such a way that the average error is halved.
- Create certainty is applying the learning procedure until the
error is less than a provided delta - the delta will be called the
certainty error.
- Adjust weights connection: in any of the cases, the process
of neuron, is able to fully connect each neuron in order to restrict to
the useful ones.
Constraints
In order to be able to serve the different types of learning, we have to
create a set of information related to the process. The set will include the
following:
- Each time the process will go to learn, we will store the inputs
along with the outputs and the time the learning was requested: multimap<
vector<output> , map< time , vector<input> > >.
- The process average error. Also, for each output we may add the
relative error associated (multimap< vector<output> , pair< Relative
error , map< time , vector<input> > > >)
- The linked process associated. We will consider it as useless to
engage a learning procedure is the process attached to this one have
their process average error n times our. and vice-versa.
- Allow a variation of the process average error the process is linked
with.
When learning?
I believe we are learning all the time and should be proud of such a
possibility. Therefore the learning procedure must be seen not as an error
reducer meaning that we will end by stopping to learn but as an excellent
way to adapt to the unexpected. We will launch the learning procedure when we know an output value is not the expected value: this
can be done in two ways:
- Some output need to be reassigned as the result of a incremental
adjustment due to contradiction I/O values (we need to discover the
contradiction I/O)
- The output resulting the evaluation does not match the reality -
this is the most complex for an application to grab as the application
cannot see, touch, hear that the conclusion it took are to be at least
adjusted.
When processes are loaded and evaluated, it is for some purpose. The process
itself has its own purpose, a collection of processes have a purpose and the
entity itself is evaluation in order to meet some answer for a purpose. But
during that process, some other process are evaluating in what we may
understand as background; also when our mind is directed in one main goal,
we still keep on thinking to other possibilities to reach the goal.
- How can we decide that one learning process on this particular process
is more important than another?
- Also how can we make sure that we have all the information to
assure to at least be able to adjust a process? Shouldn't we wait a little
bit later? As long as we are using a process, we can merely adjust
it but any other learning should only be done when we do not need it and
with all the historical constraint we were able to record.
A process is considered more important than another if the goal for which
it is evaluated is more important - we can therefore see that the importance
of the process is the meaning of its goal. I have differentiated 5 level of
importance. It is not exhaustive and therefore may be subject to more
subtle partitions.
Primary: As a remnant of our original animal part, it
serves mainly the survival: feed, reproduce, protect.
- To Feed: we have no desire to improve our way of living, we can also
eat nearly anything as long as it feeds (like Mc Donald).
- To protect: we have to preserve our corporal integrity - this may be
to avoid a car in the street or to decide running to avoid a raging
bull, etc...
- To reproduce: as the reproduction means contact, we have to preserve
a minimum of contact potential with the language, the movements and the
expression or art.
We can easily understand why these may have a very high priority and why
the results must be quite fast adjusted but later on the background must
reach the creation of certainty.
Foreground: Adjust
Background: Learn
Secondary: I call it our mammal purpose or oppose the
deficiencies our species has with the creation of a community. This
importance is in fact a complement of the primary one. Indeed we are helping
ourselves indirectly via the community. The survival of the community
becomes then a priority. In order to survive the community can for example
elect a ruler, and recognize some people as specialists in certain field of
and knowledge and production. We are forced to trust the other (the medicine
man, the chief, the baker, etc... ) and also pushed to participate to
ceremonies and public manifestation.
- Contact or create the community if none.
- Bring something to the community to make it survive. This can be as
well a job, children or a ceremony master.
- Acknowledge the specialties of others and make use of it.
- Participate to public manifestation (like concert, church, market,
... )
Foreground: Historical adjust
Background: Learn - may attempt an incremental adjust
Third: As a result of the community, the third importance
is to protect myself from abuses resulting from the community. The creation
of money (common mean of exchange) is basically the result to avoid people
to abuse situation.... As describe in the secondary level, no one could ever
avoid anyone to monopolize for himself the bread production in order to gain
power. We have then to regularize and legitimize the transactions of and
good and services. Acting so implies the protection of the goods and the
means of exchange - also a legislation and rules of behavior in order to
show example and stay impartial. Also we have to protect ourselves from
others who may via a dubious way extort money directly or indirectly. In
fact we have to protect our community from itself or some of its members;
- money is a way to avoid but also detect abuses: use it!
- respect the law and the institution of the community: use it to
protect yourself.
- help protecting your environment.
- respect and protect the ways and customs.
Foreground: Learn
Background: Historical learning - may attempt an incremental adjust
Fourth: Create via an extraction, a small community that
will protect its members from the dangers of the Community but also help
each of its members during crisis. It is the recreation of the secondary
importance not in front of the Nature but in front our our Community that as
grown too big to be controlled easily by one person.
Foreground: Historical learning
Background: Attempt an incremental adjust followed by a Historical
learning
Fifth: Learn to improve your wisdom and mind.
Foreground: Historical learning
Background: Certainty - Attempt an incremental adjust followed by a
Historical learning
Post-pone learning
There is two cases when we should post pone the learning procedure:
- When we are still using the process. it is no use to even adjust the
process as long as we are using it. In that case we have only to record
the environment/input/output in order to allow a learning procedure later.
- As we already know, some learning requests to have all the results .
This under some circumstances may require some time during which we are
allow to overview all possibilities when idle.
Utilization
|
|
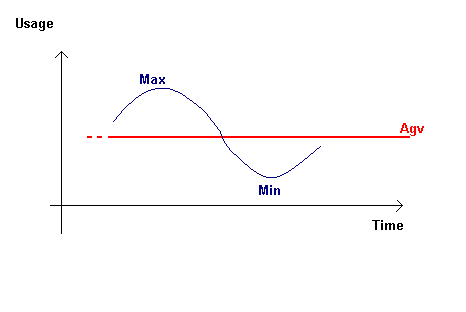 |
We may consider a
normal utilization of a process as looking like a sinusoidal shape on
the time(x)/usage(y) axis. During that period, the type of learning will
mainly follow the constraints of the importance (note that the same
process may be used in a low as well as high importance purpose)
We will recognize it by the following characteristics:
|Min - Max| is the frequency of usage, the average of frequency
of usage will be maintained and linked with the process (NB the change
of sign in the variation will trigger information on a min or max).
The last frequency (previous minima and maxima) will also be
linked to the process apart - indicating if a brutal modification
has just taken place. |
| We
will also link to the process ΔU(p): the average usage of the specific process
p. The importance will be somehow diminished or increased if the ΔU(p)
is below or above the ΔU ↔Δ∑∆U(p).
The U(p)δt (variation usage of the specific process p
during the period of time Δt) may also affect the importance.
Indeed if the absolute value of the variation difference is bigger than
the difference between the previous minima and maxima, then we should or
decrease or increase the importance of the process.
| U(p) δt | > | Max - Min |
We will not always adapt the learning type, this procedure will be
triggered under the below circumstances:
- | U(p) δt | > | Max - Min |: This process
is more and more used, we better see to improve the learning type.
- ΔU(p) > Δ∑∆U(p): for us
this process is very important and an ad hoc learning type is to be
considered.
- ΔU(p) > 0 && U(p)δt > 0: the process is to be
considered as a potential important one, we better improve it now
assuring a better service.
|
Learning type choice
We also have to adapt the learning type not only in relation with the
utilization or the importance but also to minimize the effort of learning:
the history of the learning types must also be preserved, but to what
extent? Couldn't we simply maintain average (Δ) and variation (δ) of each of
the learning type?
We will associate a map<learning type , pair< Average , pair<
Time , Variation> > > with the process. Then for each learning
type selected according to the importance of the process and the utilization
data, we will adapt the learning type according to the average and
variation.
Let us declare the following:
- ΔLT(p) as the global average of learning type requested until
now: we sum all the occurrences of the learning type for this process and
divide by the amount of time the process was used.
- ΔLT(p) δt(use) to indicate if the
average of learning for this process is increasing or decreasing.
- ΔL(type,p) is the average of a specified learning type of a
process. (ΔLT(p) is partitioned into several ΔL(type,p))
- L(type,p) δt(use) is the variation of a
specific learning type to indicate if it is increasing or decreasing.
- ΔLU(type,p) is the average of continuous utilization that did
not required a learning procedure of the type mentioned.
Let us now examine the conditions that will modify the learning type:
- ΔLT(p) δt(use) > 0
we are attempting to correct the process more and more. But the more we
correct it, the worse it get. The question resides in "isn't it improving
because we are adapting it or it just need a higher type of learning? In
order to answer we have to retrieve the current type, and verify if
L(type,p) δt(use) > 0 then we
will adapt the current learning type to a higher one.
- ΔL(type,p) > ΔLT(p): this particular learning
type has increased the general average, we will have to find out how we
can reduce the request of learning on this process.
- If the type is the highest one, we are facing a process that is very
unstable, we will then apply the type that has the lowest average
for this process hoping that it may do the trick.
- If the type is the lowest for this process, apply it! (I haven't found
a path yet!)
- Otherwise, just rerun this procedure with the next type.
- L(type,p) δt(use) > 0:
the amount of learning request has increased. we will have to know how big
this is. If ΔLU(type,p) < ΔU(p) *A (A has yet to
be determined) then we will consider that this precise learning type is
not fulfilling the learning purpose. The procedure will be reran with the
next type.
Algorithm
Let us consider the following:
- ΔW as the average of weight values for this neuron: will be
considered as small dendrite value < .25 * ΔW - a big
dendrite value >= .75 * ΔW - the
rest being considered as average dendrite value.
- δWj(t-1)
is the previous variation the dendrite has to apply.
- V(t) is the value of the soma at time t.
- VDj is the value transferred to the
dendrite j.
The algorithm will have to take two constraints into account:
- Modify as few weights as possible (change must be able to last)
- Minimize the variation to apply to the weights
When we have to learn, it means we have to improve the process answers to
fit ours. We have to adapt the weights to reduce/increase the amount of
information transferred to the last neuron. According to the variation to
apply, we are confronted with various techniques. These techniques will be
stored in memory and associated with a rate of success. We will then start
with the most popular and changes until we are completely satisfied. Then we
will store the new process.
Techniques
- In the mathematical approach, we can compute the difference, and equally partitioned it to each of
the dendrites.
" j = 1 ... n (n dendrites attached to the
neuron): Wj(t-1) * VDj = Vj(t-1)
We know that V(t-1) = ∑ Vj(t-1) and V(t) = V(t-1) +
δ => Vj(t)
= Vj(t-1) + δ/n
<=> Wj(t) = Wj(t-1)
+ (δ/n) / VDj
= Wj(t-1)
+ δ / (n * VDj)
- In the proportional approach, we will work on the δ/n expression and
use instead a more appropriate repartition of the variation. The
variation will be proportionate to the amount of value the weight has
increased the soma.
" j = 1 ... n (n dendrites attached to the
neuron): ∑wj(t-1) = ω
and δ = | v(t-1) - v(t) |
The formula could be <=> Wj(t) = Wj(t-1)
* δ / ω
But this logic will lea us to dead-ends as it will not affect the
weights of a 0 value that are stopping some value transferred.
Having V(t-1) = ∑ Vj(t-1), we can write the
formulae as followed
<=> Wj(t) = Wj(t-1)
+ δ / V(t-1)
We then here take into account not the values of the weights but the
values sent to the dendrites. It is then proportional to the values sent.
In order to adapt the weights proportionally to the weight values we
should instead compute the following:
" j = 1 ... n (n dendrites attached to the
neuron): ∑wj(t-1) * Vj(t-1) =
φ
<=> Wj(t) = [ (Wj(t-1) *
V(t-1)) + (Wj(t-1) * V(t-1)) * δ / φ) ] / V(t-1)
<=> Wj(t) = Wj(t-1)
+ (Wj(t-1) * V(t-1) * δ / φ)
/ V(t-1)
<=> Wj(t) = Wj(t-1)
+ δ * Wj(t-1)
/ φ
As this formula depend strongly on the weight value: if the previous
weight value is 0 the weight will never change... We are inclined to
accept such a behavior as we consider that resetting a weight to zero is
assigning the weight with an extreme value for extreme circumstances and
should therefore not have suddenly a weight.
If a weight has no value, it has no meaning of existence and should
there be removed from the neural pattern (creating a new pattern) - later
on, the incremental adjustment could recreate the link and adjust
the weight to a value different than zero.
- If the weight is connected to a neuron that is connected to other
neurons, it is then normal to propagate the desired variation. The
dendrite will have to propagate a certain percentage (50%) to the previous
neuron and adapt itself with 50% (= .5 * δ).
- Sometime it is better to adapt only a few dendrites. Here is a
list of philosophy to adapt one or few dendrites:
- δ > V(t-1) * .625: The variation is quite big. We can choose
several options:
- Increasing: From the small dendrites values pool,
select one randomly and adapt its weight. The same task will be done
until a historical verification will prove the choice
judicious. If the global error with the newly adapted dendrite is less
than actual then the choice is judicious.
- Decreasing: the same reasoning can be made but from the big
dendrites values pool.
- Alternative: adapt slightly all the weights of big dendrites
values.
- δ < V(t-1) * .375: the variation is relatively small, we may
then choose one of the following:
- Increasing: adapt slightly the weight of the small
dendrite values.
- Decreasing: test if we can do without one or more dendrites
- choice will be randomly and a recheck throughout the history
must verify that the removal of connection is decreasing the global
error of the process.
- δ Average:
- We have to verify if one or more big can be promoted to
average.
- or and average to small or big.
- or a small to average or big.
- Alternative: adapt slightly all the weights of big dendrites
values.
- Alternative: adapt slightly all the weights of Average
dendrites values.
What and When to use
We may enquire for the correct choice while adapting the dendrites'
ratios. But we also have an environment that will drive this choice taking
into account the importance and the learning type (meaning do we need to
adapt quickly or not?).
- Mainly an first importance require to adapt very quickly as a better
improvement will be performed later when time will allow it; and a fifth
importance gives us plenty of time to find the appropriate balance in
dendrites before reacting.
- First importance will make usage of the first technique.
- The second technique will be associated starting the secondary or
higher importance as well as back propagation.
- Adaptation will start with third importance or higher
- The current learning type is also a function of the importance but may
be seen with two levels: then one caught in the action and after during a
sort of idle. It will then adapt the technique resulting of the previous
selection.
- Adjust will mainly be associated with the mathematical
approach.
- Learning will activate the back propagation and start
with the proportional approach.
- Historical adjustment or learning will be done with the
adaptive approach.
- Incremental adjustment and the search for certainty
will choose the best approach as all of them will be verified.